Physics Department, UAM-Iztapalapa, Mexico.

Section on Molecular Transport, NIH/NICHD, U.S.

Leonardo Dagdug is Professor in the Department of Physics at the Metropolitan Autonomous University at Iztapalapa, Mexico City. He graduated in Physics from Metropolitan Autonomous University (UAM) where he also obtained a PhD in Physics. He has performed postdoctoral stays at the National Institutes of Health in USA, in the group of George Weiss. He has published over 150 papers in international journals. He has been appointed visiting at the Section on Molecular Transport (NIH/NICHD), USA.

https://orcid.org/0000-0002-2654-9267

Amazon Author Page

Qualifications

1996 – 1999 PhD Physics, UAM-Iztapalapa, Mexico.
1994 – 1995 MSc Physics, UAM-Iztapalapa, Mexico.
1989 – 1993 BSc Physics, UAM-Iztapalapa, Mexico.

Career

2005 – Present Full Professor, Physics Department, UAM-Iztapalapa, Mexico.
2021-2022 Invited Scientist, Section on Molecular Transport, NICHD, National Institute of Health, USA.
2011- 2012 Invited Scientist, Section on Molecular Transport, NICHD, National Institute of Health, USA.
2003 – 2004 Early career fellowship, Physics Department, UAM-Iztapalapa, Mexico.
2000 – 2002 Postdoctoral research associate, CIT, National Institute of Health, USA.

Grants & Awards

2000-Present National System of Researchers, SNI-III
2021 Intramural Research Program by NIH, USA.
2020 Frontier Science Grant by CONACyT, Mexico.
2013-18 Member of the Science Advisory Council of the Presidency of the Republic.
2014 Research award in the area of basic sciences and engineering by UAM, Mexico.
2012 Basic Science Grant by CONACyT, Mexico.
2010 Intramural Research Program by NIH, USA.
2005 Basic Science Grant by CONACyT, Mexico.
1999 Excellence in educational practice award, Universidad Simón Bolívar, México.

Professional Affiliations and Memberships

2021-Present Member of the National Academy of Science
2003-Present Member of the National Society of Physics

Editorial Roles

Associate Editor for Frontiers

Biophysics

Research Overview

Our research is focused on understanding diffusion in confined systems, diffusion-limited reactions and relativistic kinetic theory.

Diffusion in Confined Systems

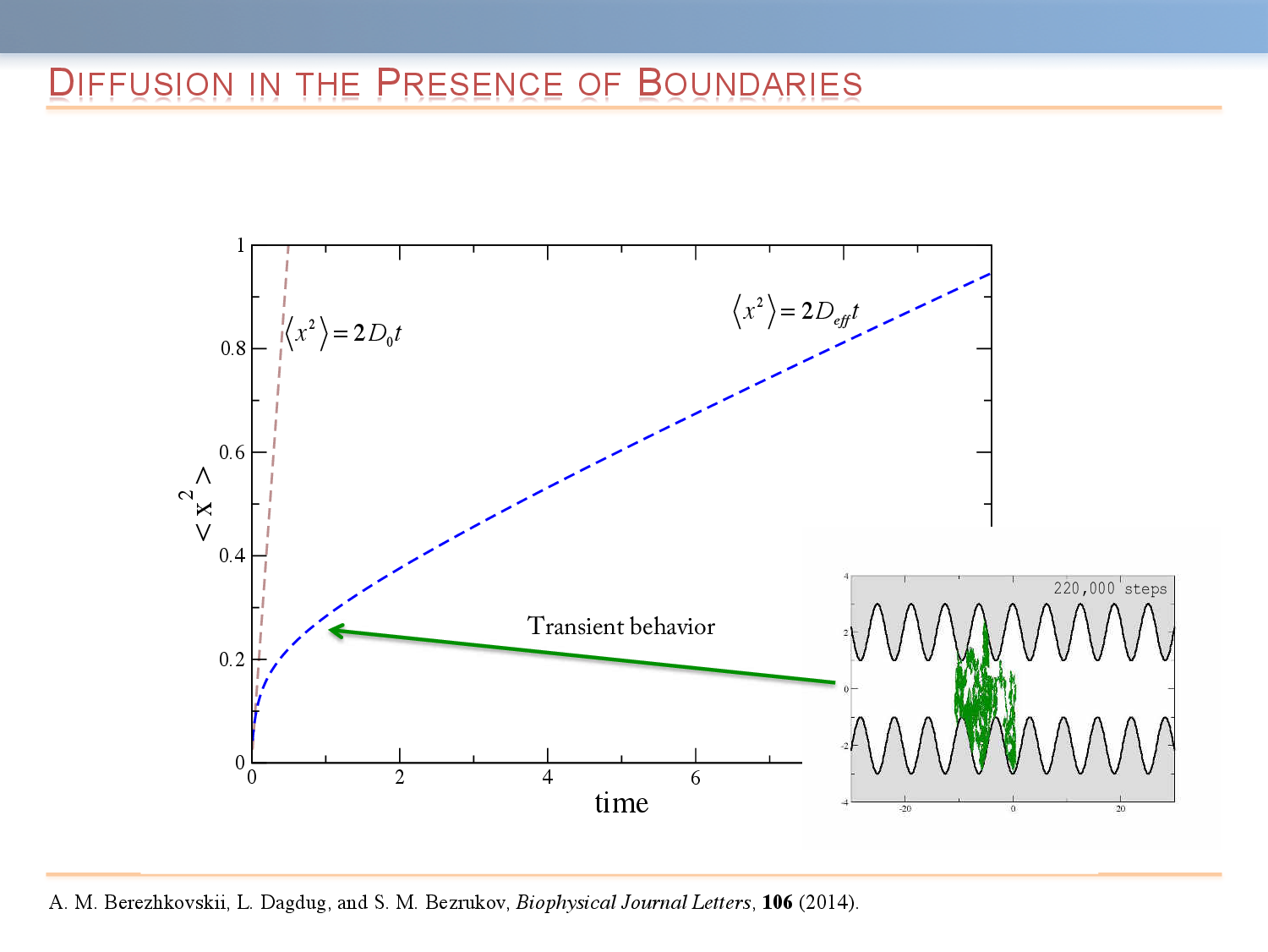
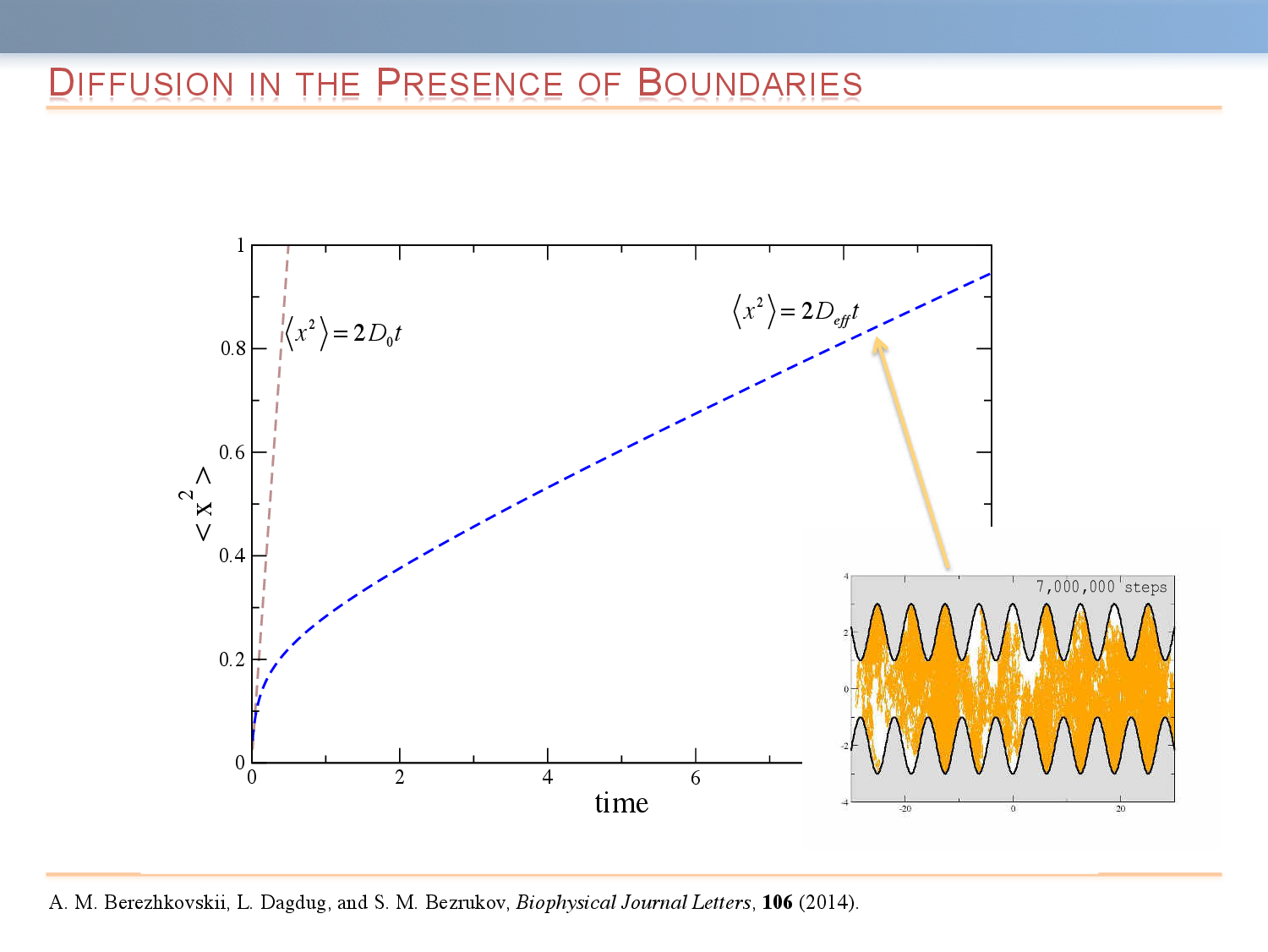
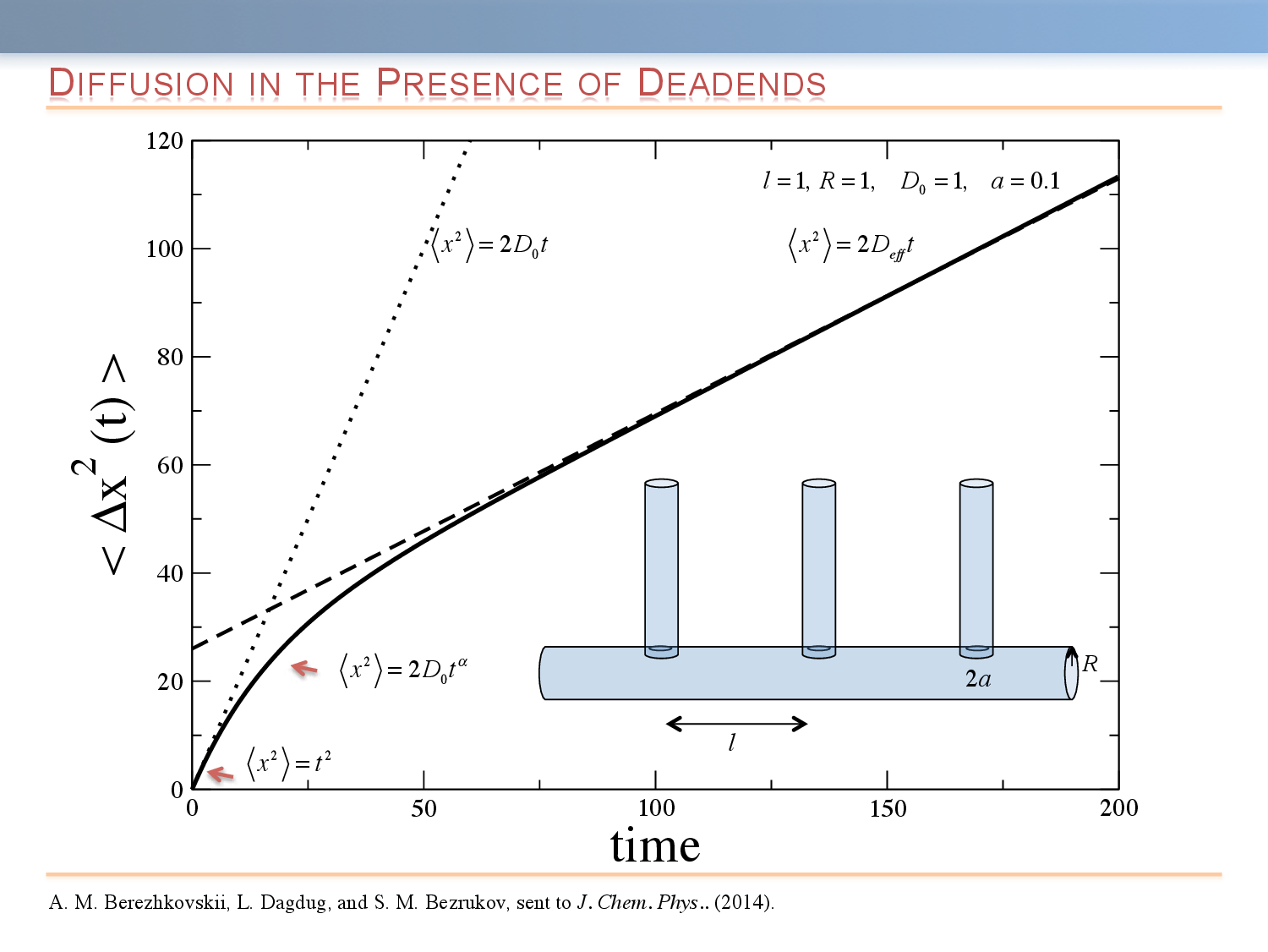
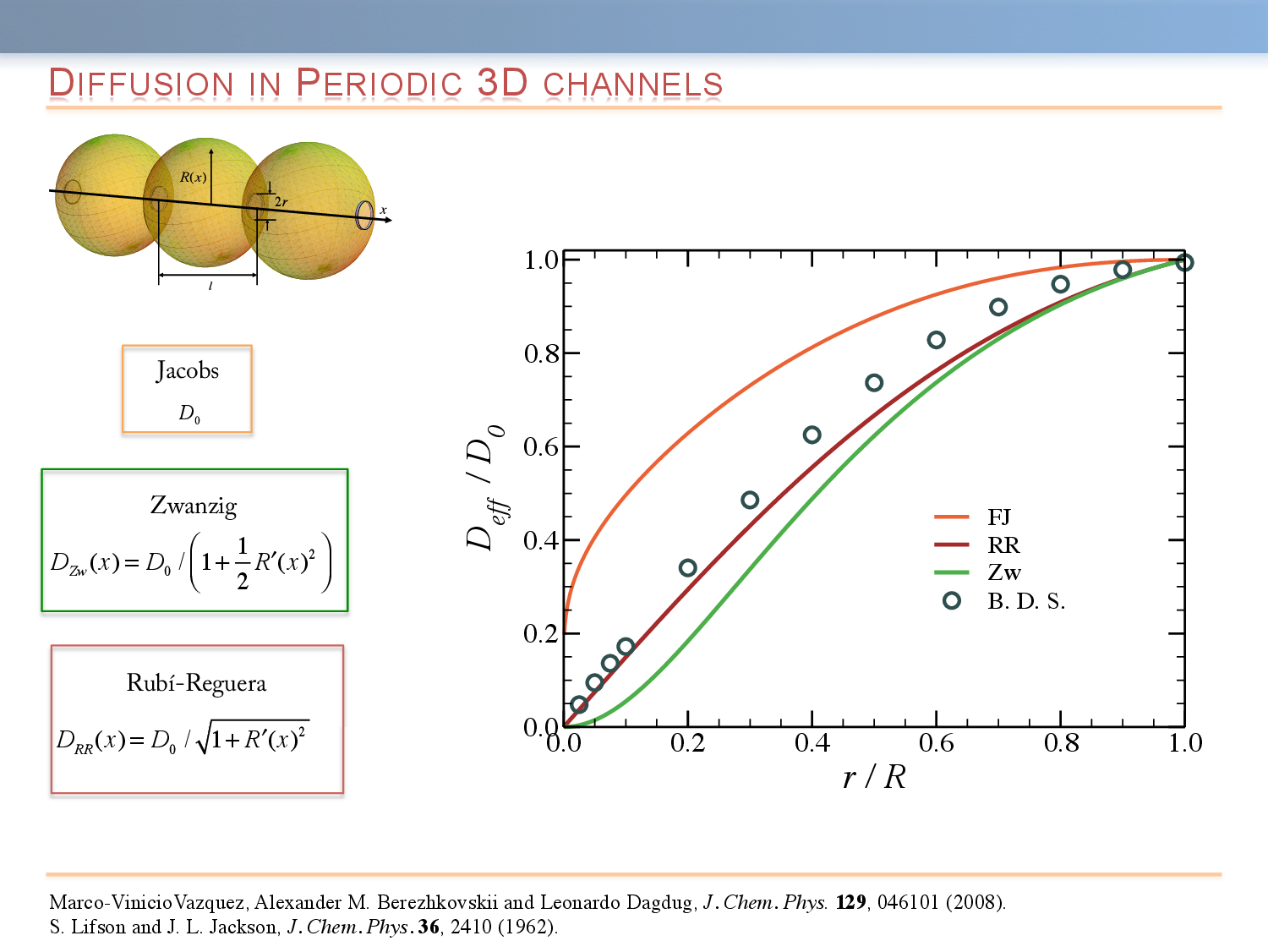
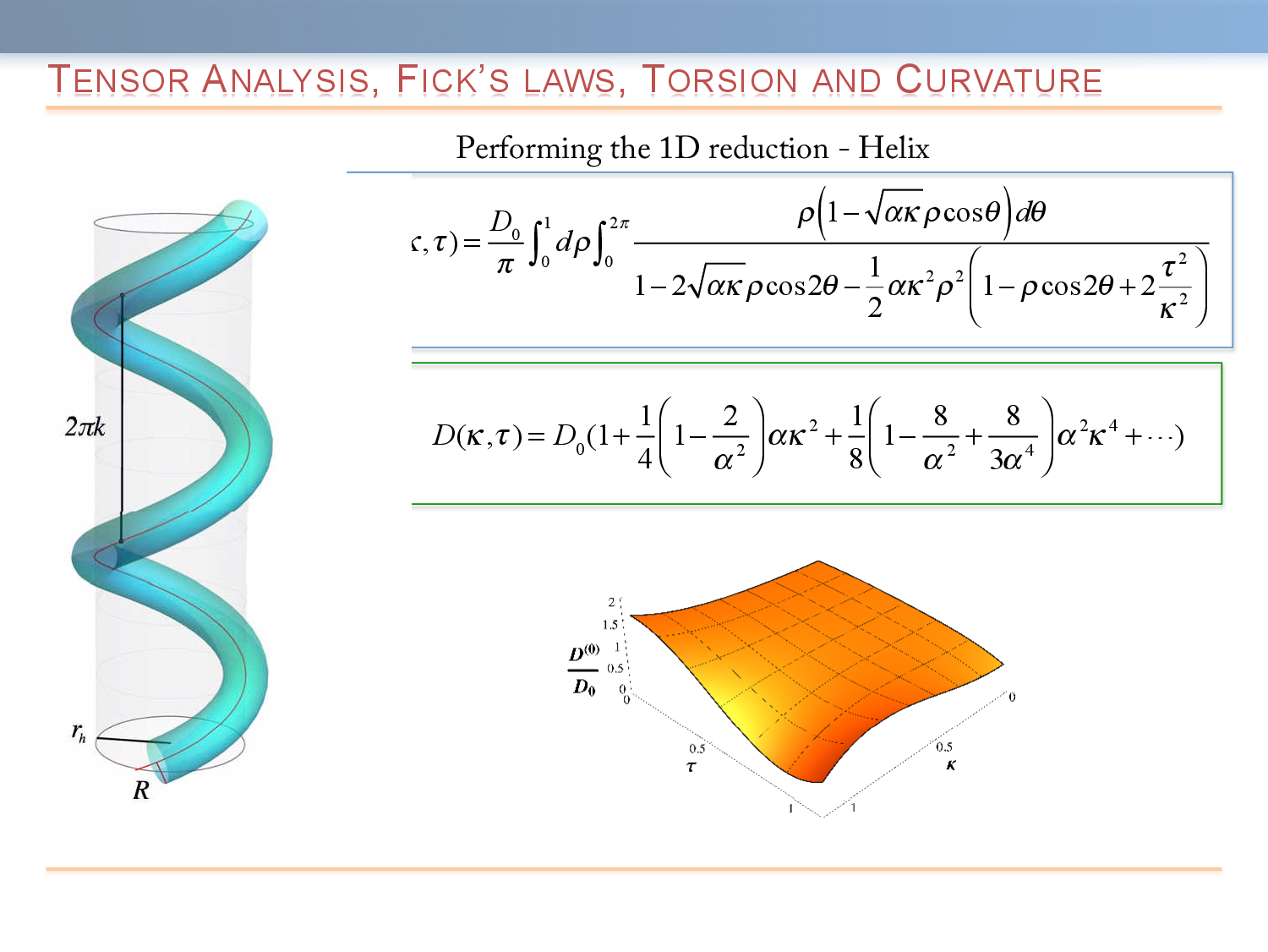
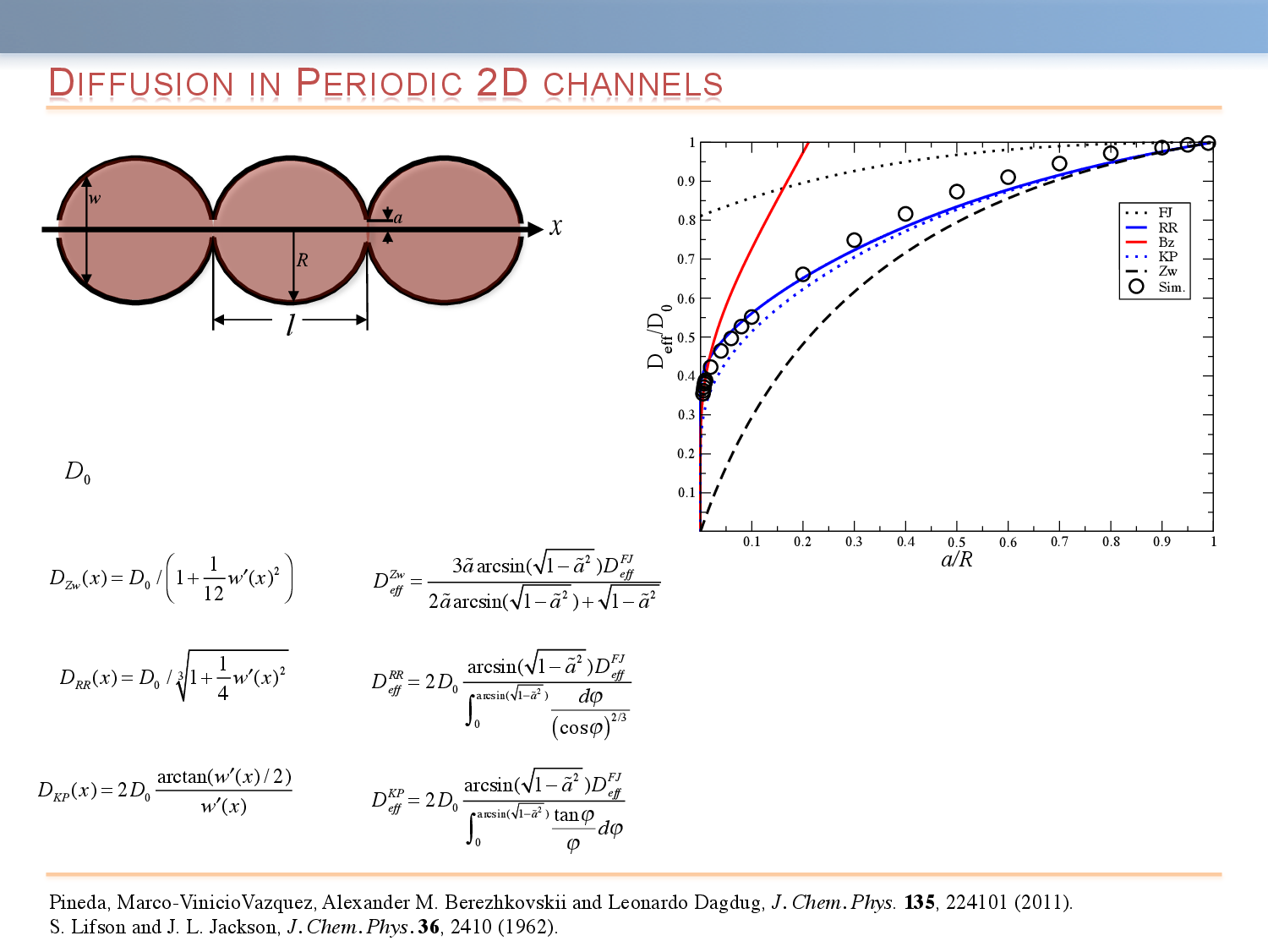
In macrohomogeneous media, a universal description of an unbiased Brownian particle is given by the free diffusion coefficient, $D_0$ . This coarse-grained description is applicable at sufficiently long times when displacement of the particle exceeds a characteristic length scale associated with the heterogeneity of the medium. On the other hand, when diffusion takes place in microheterogeneous environments, a description in terms of an effective diffusion coefficient, $D_{eff}$ , may become applicable over very long time scales. In both cases, the main characteristic of the mean-squared displacement is that it monotonically decreases from $\langle \Delta x^2 (t) \rangle = 2 D_0 t$ to $\langle \Delta x^2 (t) \rangle = 2 D_{eff}$ . One of the simplest types of non-homogeneity is confinement. The presence of the boundaries leads to a significant slowdown of mean-squared displacement.

Along with the development of experimental procedures, the problem of particle transport through confined geometries containing narrow openings and bottlenecks has led to recent theoretical efforts to study diffusion dynamics appearing in those geometries. An effective one-dimensional description of diffusion in confinement has been shown to be a useful approximation. In his original work dating back to 1855, Adolf Fick was the first scientist to treat diffusion into a channel of varying cross-sections as one-dimensional.

Earlier studies by Jacobs and Zwanzig triggered renewed research on this subject. The so-called Fick-Jacobs approach consists of eliminating transverse stochastic degrees of freedom by assuming fast equilibration in such directions. As Zwanzig pointed out, the key quantity that characterizes the speed of unbiased diffusive transport of point Brownian particles in quasi-one-dimensional systems with periodically varying geometric constraints is the effective diffusivity. As a result, enormous theoretical efforts have been made to obtain the position-dependent diffusion coefficient, $D(x)$ .

In an attempt to include different parametrizations for the midline, our group, recently proposed a covariant description of the diffusion of unbiased confined point-size Brownian particles. With this theoretical approach, one can obtain analytical expressions for $D(x)$ depending on the geometrical parameters of the confinement. In this description, the coordinate frame is placed at the tube’s axis curve, using the Frenet-Serret moving frame as the coordinate system. To describe the evolution of the probability density of particles diffusing inside the tube from this frame, they also found a transformation allowing them to write Fick’s laws in this tubular coordinates system. For narrow tubes and channels, they used an effective one-dimensional description reducing the diffusion equation to a Fick-Jacobs-like equation. From this last equation, they can calculate the effective diffusion coefficient applying Neumann boundary conditions. The expression for the effective diffusion coefficient derived depends on the position and the derivatives of the channel’s width and midline. The goal of the above-summarized theories is to establish a connection between the system’s effective diffusivity and geometrical parameters, an extremely challenging task.

Diffusion-limited Reactions

Theory of diffusion-limited reactions mainly focuses on trapping of diffusing particles by absorbers of simple shapes, while researchers and engineers often have to deal with trapping by complex-shaped absorbers. Examples include dendritic solidification of liquids and alloys, cluster growth and kinetic gelation, transport across irregular interfaces like electrodes, diffusion-limited aggregation and tumor
growth, performance of chemical reactors, etc.

Our work is focus on the description of particles trapping by complex-shaped absorbers, like patches or strips.

Diffusion With Stochastic Resetting

“Stochastic resetting” is a mechanism where a Brownian particle is stochastically reset to its initial position at a constant rate, thus driving the system away from any equilibrium state. It is thus a simple mechanism to generate a non equilibrium stationary state. “Stochastic processes subject to restart appear in many disciplines including physics, chemistry, biology, computer science. The general interest in targeting problems and their efficiency is explained by the fact that such processes find applications in a wide range of fields from chemical or biochemical reactions, diffusion processes in a cell, and searching problems in ecological environments among others. Stochastic restart may drastically reduce the expected run time of a computer algorithm, expedite the completion of a complex search process, or increase the turnover rate of an enzymatic reaction.

Our work is focus on the description of bounded Brownian particles particles with stochastic resetting.

Virus Growth and Form

A fundamental step in the replication of a viral particle is the self-assembly of its rigid capsid from its constituent proteins. The treatment of generalized physical forces driving virus growth and form is particularly challenging because of the span of the spatio-temporal scales and strengths of constitutive interactions which characterize virus assembly. At nanoscale mechanical, electrostatic, and thermal interactions, and even some biologically-important chemical bond interactions may have comparable magnitudes. It is a great challenge to understand the complex interplay between thermodynamic driving forces, mechanical stresses, and long-range electrostatic interactions driving the virus assembly. It is worth mentioning that these structural foundations can be extended to other macromolecular complex that control many fundamental processes in biology.

Our work is focus on the basic architecture of viral capsid.

Relativistic Kinetic Theory

Incorporating the relativity principles in kinetic theory is crucial not only to understand the theoretical grounds in the description of relativistic many-particles systems, but to interpret relativistic high-energy experiments like those involving heavy-ion collisions as well as phenomena in the astrophysical and cosmological realms. These include, for instance, the use of the relativistic Bolztmann equation to understand the thermal history of the universe and the structure of the cosmic microwave background radiation spectrum associated to its interaction with hot electrons in galaxy clusters.